最常见的图像压缩算法：JPEG

DIP JPEG 数字图像处理算法图像压缩哈夫曼编码

字数统计: 2.1k阅读时长: 7 min

 2024/10/22 

DIP-JPEG图像压缩

为什么JPEFG有用

人类眼镜的细胞对图像的感知程度，亮度比色度感知强烈的多。

因此减少人类眼镜感知较弱的区域，即减少颜色的差异，就可以实现压缩。

压缩步骤

首先需要进行色彩空间转换，每一个像素都有RGB的红绿蓝叠加，算法需要通过一个固定的公式算出Y（亮度）、Cb（蓝色色度）、Cr（红色色度）。
进行色度缩减取样，很多数据会被删除。将蓝色和红色色度分量层的像素按照2x2像素成一个区块这样划分。然后计算每个区块的平均值，然后缩小图像（4:2:0），使得含有1个平均值的由4个像素组成的区块只占一个像素的空间。于是那些我们👀眼睛不易感知的红蓝色度信息量shrink to 1/4 size，而亮度（luminance）保持不变。（网上流行的包浆图就是这么来的）

考虑一下刚才的两步，计算之前SIZE=1+1+1=3.0，计算之后为SIZE=1+1/4+1/4=1.5，图像已经变为原来大小的一半了。
当我们查看图像时，会放大图像到原始尺寸，根据YCbCr重新计算RGB（可能发生变化）
接下来的两个步骤是重点，进行离散余弦变换（Discrete Cosine Transform,DCT ）和量化（Quantiaztion）。这利用了人眼不擅长感知高频率的图像信息的原理，即对于细节并不能精确感知。如阴影变化，和摄影中失焦的场景。以上两个步骤会遍历图像各个部分，并找到由高频率色度或亮度的像素频繁出现的区域，然后将这些人眼很难感知的像素删除。对于三个图层中的每一个图层进行以下步骤（以亮度涂层举例）：
- 将整个图像按照8x8像素划分成许多区域，称为“区块”。每个区块因此有64像素，每个像素用0～255的数值表示。如果是亮度图层就是代表亮度值。
- 减去128来改变各个亮度数值，这样取值范围就变成了-128～-127。（亮度图-128为黑色，127为白色）
- 每一个区块内，我们可以先找到64个8x8基本图像（正弦函数的频率域图）并且每个图像都会有一个计算得出的DCT系数，原始图像可以通过计算出的每个基本图像✖️它对应的系数后再叠加64次得出。（具体的数学公式笔者也不了解，请自行网上查阅）
DCT不能压缩或缩小图像，但下一个步骤，量化可以
DCT后我们会有一个常数表，我们要把其中的各个值除上对应量化表中的各个值，并四舍五入取整。

量化表右下角数值偏高，是人眼不擅长感知德高频数据。而数值较小的左上角是人眼更容易区分的样式所在。

在刚才的步骤中，我们舍弃了人眼无法感知的数据，针对色度，我们会采用一个数值更大的量化表，舍去更多的颜色数据。

小结

从本质上讲，整个余弦变换+量化的过程，一整张图像都使用了一组相同的64个基础图像和两个量化表：一个用于亮度，另一个用于色度。以便将8x8的像素区块转换为几个数字和一大堆的0。

编码

游程编码

在这一步骤中，我们列出所有区块中的亮度与色度数值（更改后）。然而是这样的顺序：
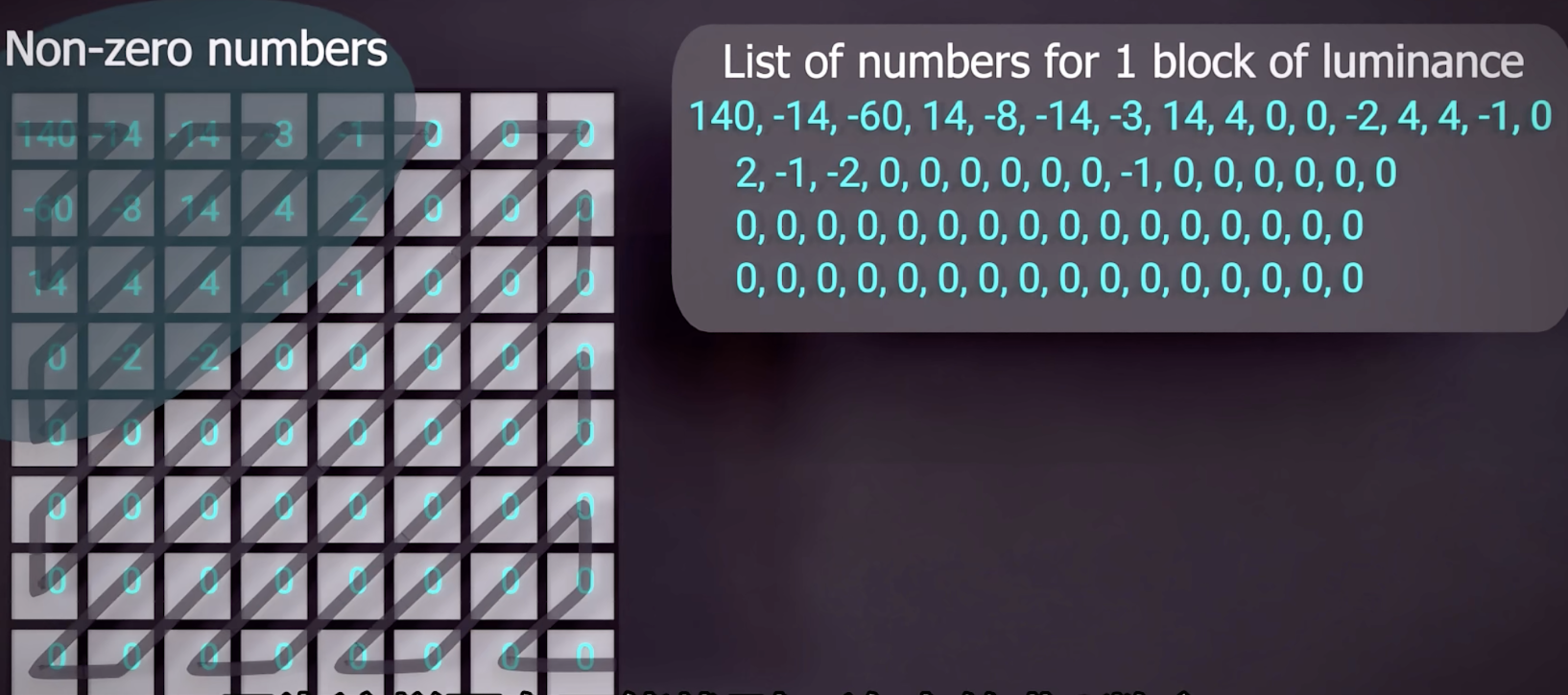
因为这样子更可能找到一连串的非0数字。
接下来，在我们列出的数字中，使用游程编码Run length encoding algorithm，列出我们有几个0。这样只有几十个数字的列表显然比0～255的方法压缩的多。

哈夫曼编码 Huffman Encoding

这种独立编码也运用在H.264视频压缩算法中（也被称为高级视频编码，AVC），是目前Youtube上传视频推荐的视频压缩算法。它使用了色度所见取样或色度抽样技术，以及离散余弦变换和量化技术的一些变种。

这里对哈夫曼编码进行简述，感兴趣的可以查阅资料自行了解。

需要对待编码的数据中每个符号出现的频率进行统计。这些频率将用于构建哈夫曼树。
哈夫曼树是一种二叉树，其中每个叶子节点代表一个符号，且路径长度与符号的频率相关。构建哈夫曼树的步骤如下：

1. 初始化：将所有符号视为独立的节点，并按照频率从小到大排序。

2. 合并最小频率的两个节点：将频率最小的两个节点合并为一个新的父节点，其频率为两个子节点频率之和。

3. 重复合并：将新节点加入节点列表中，重新排序，重复步骤2，直到所有节点合并成一棵树。
根据哈夫曼树生成哈夫曼表，从根节点到每个叶子节点的路径决定了该符号的哈夫曼编码。通常，向左分支记为0，向右分支记为1。

graph TD
Root[100]
Root --> A[45]
Root --> CBFED[55]
CBFED --> CB[25]
CBFED --> FED[30]
CB --> C[12]
CB --> B[13]
FED --> FE[14]
FED --> D[16]
FE --> F[5]
FE --> E[9]

classDiagram
class HuffmanTable {
    +Symbol : A
    +Code : 0
    +Symbol : B
    +Code : 101
    +Symbol : C
    +Code : 100
    +Symbol : D
    +Code : 111
    +Symbol : E
    +Code : 1101
    +Symbol : F
    +Code : 1100
}

H.264

然而，H.264显然更加复杂，因为它不是像JPEG那样压缩单一的静态图像。每30帧使用iFrame（JPEG），而其他29帧使用预测或双向预测,只对差异和运动进行编码，同时使用先前解码的帧作为参考。

重构图片过程

让我们回到JPEG，首先我们执行哈夫曼解码,根据哈夫曼表将编码变回DCT系数，例如：
1
2
Compressed Data: 110100010...
Decoded DCT Coefficients: [16, 11, -10, ...]
并且分解游程编码（disassemble），然后把一连串的数字按照去交错（De-Zigzag）的方式重新排列为8x8矩阵。
接下来，我们执行反量化，通俗来讲就是讲各个值乘以量化表（之前讲过的那两张表，之前是除法），然后将所得常数乘以相应的基础图像（基础图像也是一开始就有的，之前也是除法），并将所有结果图像叠加在一起。
将蓝色跟红色色度图像放大，并将亮度和色度值重新转换为RGB色彩空间。